啊……又回来了……熟悉的 DDPM 啊……

这篇文章的核心贡献在于：提出一种基于多轮 加噪 / 去噪 进行图像生成的方法框架。这种方法框架（Diffusion）在某种意义上独立于所采用的模型存在；模型所学习的是噪声——对某张带噪声图片来说，噪声最可能在哪，也即原图最可能长啥样子。

Diffusion 前最流行的图像生成方法是 GAN（标志性的工作如 StyleGAN），次一些的有 VAE（变分自编码器）、流方法、各种自回归模型等等，但它们训练效率往往极低，生成图片的质量也不很高（相对于 Diffusion 系列而言）。DDPM 作为最早的 Diffusion 方法之一并非很引人注目，但经过几轮论文周期升级而成的 DDIM、LDM / Stable Diffusion 很快展现出 Diffusion 系列方法的极高潜力，迅速席卷整个图像生成领域。

啥是 VAE？变分 自 编码器。

这里主要关注 DDPM 的数学方法及若干细节。

[2006.11239] Denoising Diffusion Probabilistic Models（2020 年 6 月）

看起来很厉害的博客 扩散模型之DDPM – 知乎

深入浅出且式子都很好理解的博客 生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼 – 科学空间|Scientific Spaces

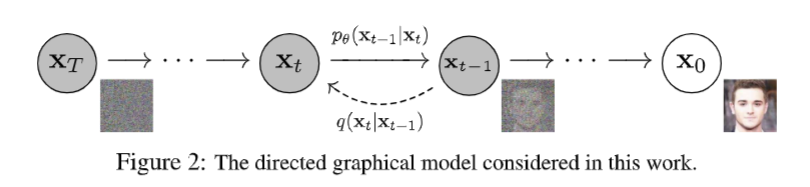
扩散过程

Diffusion 包含两个相反的过程：前向的扩散过程给一张图片加入 $T$ 次随机噪声，最终将其变为完全的纯噪声图，这个过程主要用于训练模型；反向的去噪过程给一个纯噪声图，利用模型预测 $T$ 次噪声并去噪，得到一张清晰的图片，这个过程主要用于图片生成。

加噪过程中，第 $t$ 步加入方差为 ${\beta }_t$ 的 Gaussian 噪声

$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$$

上式含义：给定第 $t-1$ 步的数据分布 $x_{t-1}\sim q(x_{t-1})$，第 $t$ 步 $x_t\sim q(x_t)$ 的数据分布由在前一步的数据上加随机 Gaussian 噪声决定。

具体操作是

$$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_t,{ϵ}_t\sim \mathcal{N}(0,I)$$

所有 ${\beta }_t$ 被预先确定。

为什么 $x_{t-1}$ 要乘一个 $\sqrt{1-{\beta }_t}$？因为希望 $x$ 的方差一直是 $I$，这样最后得到的噪声图接近很简洁的 $x_T\sim \mathcal{N}(0,I)$。

一个重要的事实是，由于 Gaussian 分布的可加性，$t$ 步加噪可以一并完成。记 ${\alpha }_t=1-{\beta }_t$，推一下得到

$$x_t=\sqrt{\prod _{i=1}^t{\alpha }_i}{x}_0+\sqrt{1-\prod _{i=1}^t{\alpha }_i}ϵ,ϵ\sim \mathcal{N}(0,I)$$

再记 ${\overline{\alpha }}_t=\prod _{i=1}^t{\alpha }_i$ 则可以简单地写作 $x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ$。

然后 $x_0\sim q(x_0)$ 也看作方差为 $0$ 的 Gaussian 分布 $\mathcal{N}(x_0,0)$，这样 $x_t\sim \mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,1-{\overline{\alpha }}_t)$。这就是 $q(x_t|x_0)$。

理想去噪过程

去噪过程中，第 $t$ 步去掉刚刚加上的随机变量……

等等！随机变量怎么可能“去掉”？毕竟我们也不知道它是多少啊！就算我们尝试用模型去预测加噪过程第 $t$ 步加的 ${ϵ}_t$ 长啥样，最后也只会训出一个只输出 Gaussian 噪声的模型（因为当时加上的就是一个 Gaussian 分布的随机变量）……

不管怎样，由于 Gaussian 分布的可加性，我们知道 $x_{t-1}$ 肯定服从某个 Gaussian 分布。

来一个 Bayes：

$$q(x_{t-1}|x_t,x_0)=\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}q(x_t|x_{t-1})$$

为啥要再考虑 $x_0$？因为 $x_{t-1}$ 是由 $x_0$ 生成的，没有单独的 $q(x_{t-1})$，或者说，当我们写出 $q(x_{t-1})$ 时，其实就自带为 $q(x_{t-1}|x_0)$ 了。

或者说，这里讨论的是理想去噪过程，在仅知道一张噪声图 $x_t$（而不知道原图可能有哪些）的情况下当然不可能理想地恢复原图。

模型到时候会在图片集上训练，尝试做到仅根据输入的 $x_t$ 恢复原图。我们把这个过程记作模型去噪过程 $p_{\theta }(x_{t-1}|x_t)$，以与理想去噪过程区分。

那为啥最后那项没有 $x_0$？带上也行，但由 Markov 链的原因，$x_t$ 只和 $x_{t-1}$ 相关所以多此一举。

（现在我还不知道要干啥……但可以把前面的东西代进来所以就代吧）

利用 Gaussian 分布的密度函数（省略 $\exp$ 前的常数项）$\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$ 代入之前结果：

$$\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =\exp (-\frac{1}{2}(\frac{(x_t-{\sqrt{\alpha }}_t{x}_{t-1}{)}^2}{1-{\alpha }_t}-\frac{(x_t-\sqrt{{\overline{\alpha }}_t}{x}_0{)}^2}{1-{\overline{\alpha }}_t}+\frac{(x_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\overline{\alpha }}_{t-1}}))\\ & =\exp (-\frac{1}{2}((\frac{{\alpha }_t}{1-{\alpha }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})x_{t-1}^2-(\frac{2{\sqrt{\alpha }}_t{x}_t}{1-{\alpha }_t}+\frac{2\sqrt{{\overline{\alpha }}_{t-1}}{x}_0}{1-{\overline{\alpha }}_{t-1}})x_{t-1}+c))\end{array}$$

后面 $c$ 是一坨常数。鉴于之前已经省略常数项了，并且大家推到这的时候也自动省略 $c$ 了我们也就不管它了。

为什么要化成这样？因为我们已经知道，$x_{t-1}$ 服从某个 Gaussian 分布，化成上面的样子再配方一下可以把这个 Gaussian 分布的均值 ${\tilde{\mu }}_t$ 和方差 ${\tilde{\beta }}_t$ 求出来。它们是：

$$\begin{array}{rl}{\tilde{\mu }}_t& =\sqrt{{\alpha }_t}\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}{x}_t+\sqrt{{\overline{\alpha }}_{t-1}}\frac{1-{\alpha }_t}{1-{\overline{\alpha }}_t}{x}_0\\ {\tilde{\beta }}_t& =\frac{(1-{\overline{\alpha }}_{t-1})(1-{\alpha }_t)}{1-{\overline{\alpha }}_t}\end{array}$$

注意到方差是一个常数，这是自然的。均值则是一个关于 $x_t$ 和 $x_0$ 的函数。也就是说，在理想去噪过程中，我们在知道 $x_0$ 的情况下，可以这样根据 $x_t$ 弄出一个分布，然后采样 $x_{t-1}$。

模型去噪过程

对 $p_{\theta }(x_{t-1}|x_t)$ 呢？我们希望它与 $q(x_{t-1}|x_t,x_0)$ 越接近越好。设 $p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\mathrm{\Sigma }}_{\theta }(t))$，由之前的讨论方差是个常数，所以可以不让模型管这些，${\mathrm{\Sigma }}_{\theta }(t)={\tilde{\beta }}_t$。

衡量两个分布的“接近程度”有 KL 散度，我们计算 $p_{\theta }$ 和 $q$ 的 KL 散度看看要优化的目标是啥：

$$D_{KL}(q\parallel p_{\theta })=\frac{1}{2}(\frac{1}{{\tilde{\beta }}_t}\parallel {\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t){\parallel }^2)$$

KL 散度（Kullback-Leibler Divergence）是衡量两个分布之间差异的方法，广泛运用于机器学习等领域。它有一个不那么唬人的名字叫“相对熵”。

$$D_{KL}(P\parallel Q)={\int }_{x}P(x)\log \frac{P(x)}{Q(x)}dx$$

注意到这个式子是不对称的！！其中，$P$ 是真实分布，$Q$ 是近似分布。

对两个 Gaussian 分布来说，KL 散度可以用以下式子计算：

$$KL(p_1\parallel p_2)=\frac{1}{2}(\text{tr}({\mathrm{\Sigma }}_2^{-1}{\mathrm{\Sigma }}_1)+({\mu }_2-{\mu }_1{)}^T{\mathrm{\Sigma }}_2^{-1}({\mu }_2-{\mu }_1)-n+\log \frac{det{\mathrm{\Sigma }}_2}{det{\mathrm{\Sigma }}_1})$$

好难推……ML 研究的数学爆算浓度这么高吗……

无论如何，上面 $p_{\theta }$ 和 $q$ 的 KL 散度就是直接代入上式的结果。

把这个作为优化目标就行啦。

$$L={\mathbb{E}}_{q(x_t|x_0)}[\frac{1}{2{\tilde{\beta }}_t}\parallel {\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t){\parallel }^2]$$

但是但是！DDPM 发现这样效果不好，因此实际不是这样干的。之前得到一个这样的式子：

$$x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,ϵ\sim \mathcal{N}(0,I)$$

在已知 $x_t$ 的情况下，可以用 $ϵ$ 把 $x_0$ 换掉！这个做法被称为重参数化。把上面的 ${\tilde{\mu }}_t$ 展开，然后换掉 $x_0$ 得到

$$L=\mathbb{E}[\frac{1}{2{\tilde{\beta }}_t}\parallel \frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}ϵ)-{\mu }_{\theta }(x_t,t){\parallel }^2]$$

对 ${\mu }_{\theta }$ 也进行重参数化

$${\mu }_{\theta }=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta })$$

现在不让模型预测 $\mu$，而是预测 $ϵ$，把上面的东西丢到 $L$ 里得到

$$L=\mathbb{E}[\frac{(1-{\alpha }_t{)}^2}{2{\tilde{\beta }}_t{\alpha }_t(1-{\overline{\alpha }}_t)}\parallel ϵ-{ϵ}_{\theta }(x_t,t){\parallel }^2]$$

再次地，不管前面那一坨常数，得到最终的优化目标：

$$L=\mathbb{E}[\parallel ϵ-{ϵ}_{\theta }(x_t,t){\parallel }^2]$$

真好。

所以还是要预测噪声，但噪声不是一个满足 Gaussian 分布的随机变量吗？

考虑 $ϵ$ 的意义：每次拿一张图片训练时对 $x_0$ 加 $t$ 步噪声之后得到 $x_t$，这 $t$ 步噪声组合在一起是 $ϵ$。虽然分布 $p(ϵ|x_t)$ 确实是一个 Gaussian 分布，但在已知 $x_0$ 的情况下 $p(ϵ|x_t,x_0)$ 所包含的信息量等价于 $q(x_{t-1}|x_t,x_0)$，即，在已知 $x_t$ 和原始图片集的情况下，预测噪声与预测加噪之前的图片等价。

总感觉论文作者的实际情况是先拍脑袋想出了这个优化目标，然后根据 KL 散度和之前 VAE 工作的范式证明了它的正确性……

毕竟其中有大量“舍弃常数”的操作，如果仅关注关键变量的流向的话，对 $ϵ$ 的 $L_2$ 误差、对 $\mu$ 的 $L_2$ 误差和对原始 Gaussian 分布的 KL 散度这三个目标在直观上看是极为相似的。

回顾一下这串推导都在干啥，毕竟我们似乎只是从一堆显然的事实推出了另一些显然的事实：

• 首先已知 $x_t$ 和 $x_0$ 的话（理想情形）可以推出 $x_{t-1}$，对 $x_{t-1}$ 的分布有一个描述；
• 但图片生成的时候肯定不能知道 $x_0$，因此希望模型基于 $x_t$ 预测的 $x_{t-1}$ 分布和理想情形的 $x_{t-1}$ 分布越接近越好，这是我们的原始优化目标，但这个显然没法算；
• 我们用爆算证明了这三个优化目标在忽略常数的情况下等价：
  • （VAE 的观点）$p_{\theta }(x_{t-1}|x_t,t)$ 和 $q(x_{t-1}|x_t,x_0)$ 的 KL 散度；
  • （基于图片的误差）${\mu }_{\theta }(x_t,t)$ 和 $\tilde{\mu }(x_t,x_0)$ 的 $L_2$ 误差；
  • （基于噪声的误差）${ϵ}_{\theta }(x_t,t)$ 和 $ϵ$ 的 $L_2$ 误差。
• 然后发现最后一个优化目标实践中最方便，就用它了，直观上看着也挺合理。

如何训练？如何采样？

得到了上面那个优化目标之后训练的过程就非常简洁了。

Step 1 取一张图片 $x_0$，指定一个 $t$，随机产生一个 $ϵ\sim \mathcal{N}(0,I)$。

Step 2 计算 $x_t$。

Step 3 把 $x_t$ 和 $t$ 丢进模型预测一个 ${ϵ}_{\theta }$，与 $ϵ$ 比较计算 $L_2$，然后计算梯度更新网络。

采样过程也顺水推舟地出来了。

Step 1 随机产生一个 $x_T\sim \mathcal{N}(0,I)$。

Step 2 对 $t=T,\cdots ,1$，$x_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))$。可以加点随机性，给上式后面补一个 $+{\alpha }_{t}z,z\sim \mathcal{N}(0,I)$。

Diffusion 的常用网络结构是基于 Attention 层和 Residual 块搭建的 U-Net，同时引入对时间步的编码。

实际采样过程中取的 $T$ 往往较大，论文中取 $T=1000$。