非常现代的技术。虽然现在也有点入土了。

3DGS 这个名字几乎把整片论文概括其中：任务类型是三维重建；表示场景的方法是一组 Gaussian 分布，可以理解成边缘糊糊的椭球；Splatting 是渲染方法，通过把这一堆 Gaussian 分布“泼”到一个二维平面上完成渲染，很有光栅化的味道。

3DGS 的效果是相当强大的，在给定多张不同视角的图片下，其同时实现了：对场景的渲染（而非单个物体）、1080p、实时渲染（$\ge$ 30fps）。

arxiv.org/pdf/2308.04079（2023 年 8 月）

写的很好的博客：一文带你入门 3D Gaussian Splatting – 知乎

3D Gaussian

3D Gaussian 长这样：

$$G(x)=\alpha \exp (-\frac{1}{2}{x}^T{\mathrm{\Sigma }}^{-1}x)$$

容易发现这是一个（不考虑位置 $\mu$ 的）三维正态分布，前面一坨系数被用一个额外参数 $\alpha$ 代替，这个 $\alpha$ 被认为描述了不透明度。此外还应该有一个球谐函数 $c$ 表示各个方向观察到的颜色，暂不考虑。

在点云表示中，一个场景被理解为一个疏密不均的点集；Gaussian 表示只是把点云中的点都换成了 3D Gaussian，就像在每个点的附近笼上一个电子云。

理论上协方差 $\mathrm{\Sigma }$ 可以长成任何一个半正定矩阵，但这里我们假设其可以被一个仿射变换描述

$$\mathrm{\Sigma }=RS{S}^T{R}^T$$

其中 $R$ 是一个旋转，$S$ 是一个缩放，它们可以分别用一个四元数 $q$ 和一组缩放系数 $s$ 描述。

为啥这么假设？到时候网络要学的东西就是这个 $\mathrm{\Sigma }$，如果直接优化 $\mathrm{\Sigma }$ 的话难以保证半正定，拆成这样的话每一步都是可微的，优化目标可以传到 $q$ 和 $s$ 上，又能保证正定性。

如果 $\mathrm{\Sigma }$ 是单位阵的话可以想象这个 3D Gaussian 会长得像一个边缘模糊的球；在上述 $\mathrm{\Sigma }$ 的简化下自然就像一个椭球了。

综上一个不考虑颜色的 3D Gaussian 需要 11 维参数描述：$\alpha$，位置 $\mu$，两个协方差矩阵参数 $q$ 和 $s$。流程中的每个参数都是可微的。论文里面甚至细致地推了它们的微分式子

3DGS 的输入是 SfM 结构化处理（Structure from Motion）后的一组多视角图片带相机位姿。SfM 的副产物是一个描述场景的稀疏点云，3DGS 就在这个点云的点上计算并优化 Gaussian。

啥是 SfM？

用摄像机给场景录一段视频，逐帧抽出图像，SfM 可以还原出每帧对应的相机位姿，顺便得到一个稀疏点云。SfM 一般基于经典的特征点匹配技术实现，对每帧找特征然后追踪这些特征点的移动情况。

到时候会利用梯度下降等方法学习 每个 Gaussian 的各个参数。

作为 Gaussian 基础的点云并不是一成不变的。可以通过自适应密度控制等方式加点删点等。

Splatting

首先是把所有世界空间的 Gaussian 变到相机空间里面，给一个视图变换 $W$ 和一个投影的情况下：

$${\mathrm{\Sigma }}^{\prime }=JW\mathrm{\Sigma }{W}^{-1}{J}^{-1}$$

$J$ 是投影变换的 Local affine approximation 近似（啥玩意看不懂，先这么写着吧感觉是经典技术）的 Jacobian 矩阵。这样处理的好处是，3D Gaussian 变换完之后变成的还是 3D Gaussian。

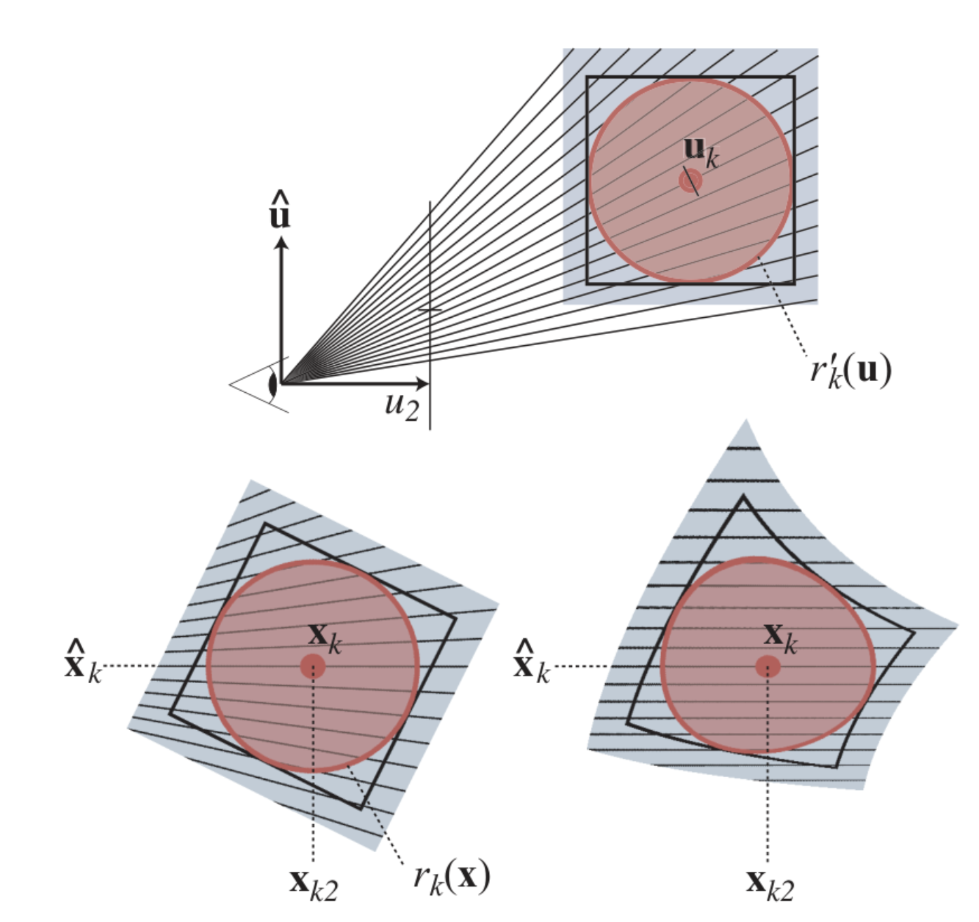
其它的照常计算。特别地，投影得到的 Gaussian 的不透明度 $\alpha$ 不再是原来的 $\alpha$，需要手推一遍。

可以想见之后会有一个类似 Alpha Blending 的过程，里面会对所有 3D Gaussian 在整个光程积分然后求和。一个小 Trick 在于这里实际上不用真的去数值积分：3D Gaussian 的积分就是 2D Gaussian，其协方差矩阵也可以直接算出来。

并且如果沿正确的方向积分的话，新的协方差矩阵只需要把原来的丢掉一行一列就行了。

网上有人说这一步很妙。妙在哪了……概率论没学好吧……

之所以选择 Gaussian 函数作表示会不会就是因为它积起来很方便（并且有直观意义）？

然后按深度排序，Alpha Blending 渲染一下

$$C=\sum _{i=1}^n{c}_i{\alpha }_i^{\prime }\prod _{j=1}^{i-1}(1-{\alpha }_j^{\prime })$$

其中 ${\alpha }_i^{\prime }$ 被如下计算：

$${\alpha }_i^{\prime }={\alpha }_{i}G(x,{\mu }_i)$$

其中 ${\mu }_i$ 是第 $i$ 个 Gaussian 的位置，$G$ 是 2D Gaussian。

注意到每个 Gaussian 长得像个球但实际弥散到了整个空间，对每个像素点把全体 Gaussian 过一遍的话开销太大。一个基本想法是，把屏幕空间划分为一堆 Tile，对每个 Tile 仅考虑里面的 Gaussian。